Исследование графика функции

Сегодня мы рассмотрим возможности Geogebra по исследованию графиков функции: нахождение нулей и экстремумов, а также построение касательной к точке экстремума.
Исследуйте график кубической функции f(x) = a x³ + b x² + c x + d, где a, b, c и d – это параметры, значения которых меняются с помощью ползунков.


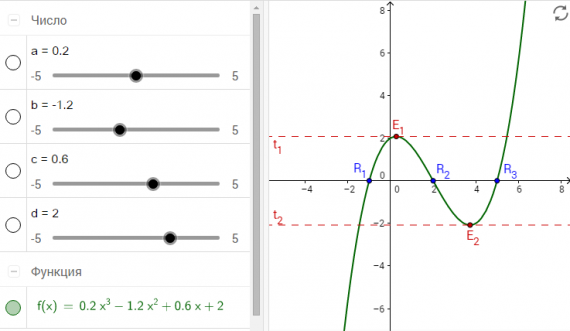
ИНСТРУКЦИЯ

1	f(x)	Введите f(x) = a*x³ + b*x² + c*x + d в поле алгебраического ввода и нажмите кнопку Enter. Подсказка: GeoGebra автоматически создаст ползунки для параметров.
2		Скройте ползунки a, b, c и d нажатием на синий кружок слева от их координат в окне алгебраического вида.
3		В окне Алгебраического вида установите значения параметров, на значение, которые соответствуют изучаемой функции, например a = 0.2, b = -1.2, c = 0.6 и d = 2.
4	Root[f]	Введите команду R = Root[f] или на русском языке R = Корень[f], для отображения нулей функции R1, R2 и R3.
5	Extremum[f]	Введите команду E = Extremum[f] (или E = Экстремум(f)) для отображения экстремумов функции.
6		Используя инструмент Касательная, постройте касательные к графикам функции в точках экстремума E1 и E2. Подсказка: Выберите точку E1 и график функции для создания касательной. Повторите действия для точки E2.
7		Изменяйте значения параметров для исследования функции.