Компьютерный эксперимент в Geogebra
Сегодня мы поговорим о возможностях Geogebra по проведению компьютерного эксперимента. Стоит отметить, что под компьютерным экспериментом здесь понимается разновидность модельного эксперимента, в котором в качестве объекта изучения выступает динамический чертеж (модель).
А.В. Середа в своем учебном пособии «Техника решения планиметрических задач» пишет: «Главной идеей применения на уроках любой программы, реализующей идеи динамической геометрии, является «открытие» учащимися геометрических закономерностей, возможность проведения компьютерного геометрического эксперимента… При варьировании динамического чертежа гораздо легче выделить те свойства рассматриваемой конфигурации, которые являются неизменными, т.е. следствия условий, накладываемых на исходную фигуру, – например, заметить, что какие-то прямые всегда параллельны или какие-то отрезки равны. Компьютерный эксперимент может подсказать решение задачи, а может помочь опровергнуть какие-то предположения, кажущиеся вполне правдоподобными».
Рассмотрим несколько примеров проведения компьютерного эксперимента на уроках геометрии с помощью надстройки Geogebra.
Проверить верность предположения, можно путем создания динамического текста.
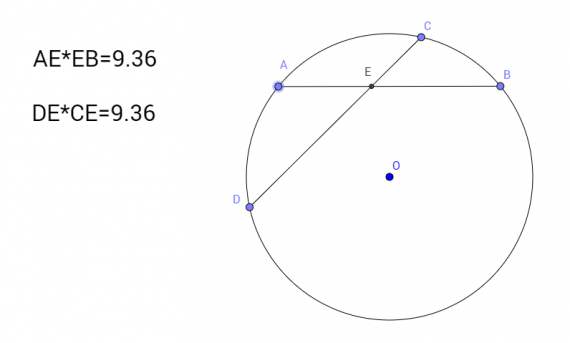
Рис 1. Рабочий лист с построением и динамическим текстом, подтверждающим догадку
Очень важным является понимание учащимися того, что это еще не доказательство. Для того чтобы подтвердить гипотезу, необходимо воспользоваться соответствующими теоремами планиметрии, в данном случае, опираясь на свойство подобных треугольников.
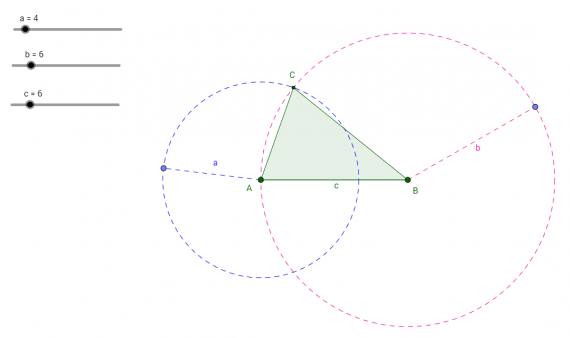
Рис 2. Рабочий лист «Неравенство треугольника»
Подробнее рассмотрим технологию создания такого динамического листа:
Исследовать с помощью Geogebra условия существования треугольника, заданного двумя сторонами и медианой, проведенной к одной из них.
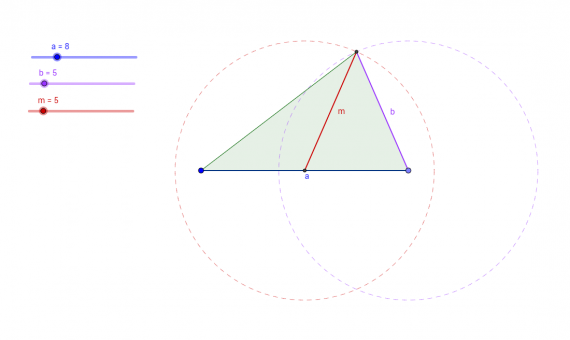
Рис 3. Рабочий лист «Существование треугольника (по 2 сторонам и медиане»
А.В. Середа в своем учебном пособии «Техника решения планиметрических задач» пишет: «Главной идеей применения на уроках любой программы, реализующей идеи динамической геометрии, является «открытие» учащимися геометрических закономерностей, возможность проведения компьютерного геометрического эксперимента… При варьировании динамического чертежа гораздо легче выделить те свойства рассматриваемой конфигурации, которые являются неизменными, т.е. следствия условий, накладываемых на исходную фигуру, – например, заметить, что какие-то прямые всегда параллельны или какие-то отрезки равны. Компьютерный эксперимент может подсказать решение задачи, а может помочь опровергнуть какие-то предположения, кажущиеся вполне правдоподобными».
Рассмотрим несколько примеров проведения компьютерного эксперимента на уроках геометрии с помощью надстройки Geogebra.
Пример 1. Изучение свойств хорд окружности
На динамическом чертеже, с указанием длин отрезков. Меняя положение точек на окружности, можно проверять соотношения длин отрезков для разных хорд, до тех пор пока не будет замечена закономерность: AE• BE=CE • DEПроверить верность предположения, можно путем создания динамического текста.

Рис 1. Рабочий лист с построением и динамическим текстом, подтверждающим догадку
Очень важным является понимание учащимися того, что это еще не доказательство. Для того чтобы подтвердить гипотезу, необходимо воспользоваться соответствующими теоремами планиметрии, в данном случае, опираясь на свойство подобных треугольников.
Пример 2. Неравенство треугольника.
Несмотря на то, что неравенство треугольника в геометрии это одно из интуитивных свойств расстояния, утверждающее, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Тем не менее, не всегда учащимся легко уловить его суть, а средства GeoGebra позволяют наглядно проиллюстрировать это свойство.
Рис 2. Рабочий лист «Неравенство треугольника»
Подробнее рассмотрим технологию создания такого динамического листа:
- Создайте ползунки a, b и c, используя инструмент Ползунок. Установите минимальное значение 0, а максимальное – 10, с шагом 0.5
- Используя инструмент Отрезок с фиксированной длиной, постройте отрезок в любой точке плоскости длиной с.
- Постройте окружность с центром в точке А радиусом b, и окружность с центром в точке В радиуса a, используя инструмент Окружность по центру и радиусу.
- Обозначьте точку С, как точку пересечения окружностей, используя инструмент Пересечение.
- Постройте треугольник АВС, используя инструмент Многоугольник.
- Используя инструмент Указатель, меняйте значения параметров, и проследите за изменениями в чертеже.
 Самостоятельно попробуйте
Самостоятельно попробуйте
Исследовать с помощью Geogebra условия существования треугольника, заданного двумя сторонами и медианой, проведенной к одной из них.
Рис 3. Рабочий лист «Существование треугольника (по 2 сторонам и медиане»
0 комментариев