Возможности использования ползунка в Geogebra для задания параметров

Сегодня мы рассмотрим несколько вариантов использования ползунка в Geogebra:
1. Изучение графика линейной функции
2. Построение графика функции с модулем f(x) = |x| и изучение точек пересечения с графиком функции g(x)=a
3. Графическое решение линейного неравенства ax + b ≤ c

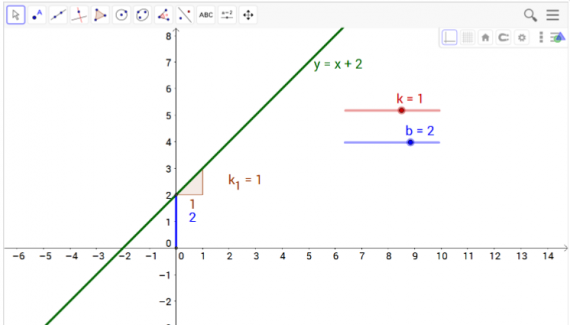
Построение графика функции с параметром

1. Постройте график линейной функции y = k x + b, где k и b – это параметры, значения которых меняются с помощью ползунков
2. Визуализируйте величины, зависимые от параметров (угол наклона к оси Х и смещение относительно начала координат).

ИНСТРУКЦИЯ

1		Используя виртуальную клавиатуру, введите уравнение линейной функции y = k x + b в поле алгебраического ввода и нажмите кнопку Enter. Подсказка: GeoGebra автоматически создаст ползунки для параметров k и b.
2		Создайте точку A, как пересечение прямой и оси y. Подсказка: Вы можете использовать как инструмент Пересечение, так и команду Intersect(a, yAxis).
3		Создайте точку В как пересечение осей координат.
4		Используя инструмент Отрезок постройте отрезок, соединяющий точки A и B. Подсказка: Вы также можете использовать команду Segment[A, B]
5		Скройте точки A и B нажатием на синий кружок слева от их координат в окне алгебраического вида.
6		Используя инструмент Наклон прямой, покажите угол наклона прямой к оси ординат.
7		Используя панель Стили, повысьте наглядность вашего чертежа (например, увеличьте толщину и цвет отрезка АВ).

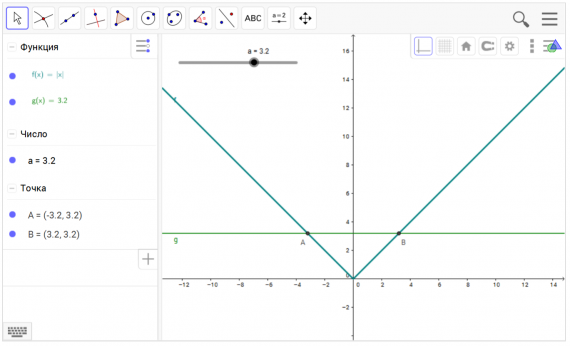
Построение графика функции с модулем

1. Постройте график функции с модулем f(x) = |x|
2. Найдите точки пересечения графика функции f(x) и g(x)=a, где а –параметр, значение которого можно изменять.

ИНСТРУКЦИЯ

1	f(x)	Используя виртуальную клавиатуру, введите уравнение функции f(x) = abs(x) в поле алгебраического ввода и нажмите кнопку Enter. Подсказка: В GeoGebra модуль вводится как abs().
2		Создайте ползунок a, используя инструмент Ползунок. Установите минимальное значение 0, а максимальное – 5, с шагом 0.1.
3	g(x)	В окне Алгебраического вида введите команду g(x)=a.
4		Создайте точки A и В как точки пересечения графиков функций, используя инструмент Пересечение. Подсказка: вам потребуется использовать инструмент пересечения дважды, для того, чтобы обозначить обе точки
5		Изменяйте значения параметра для исследования функции.

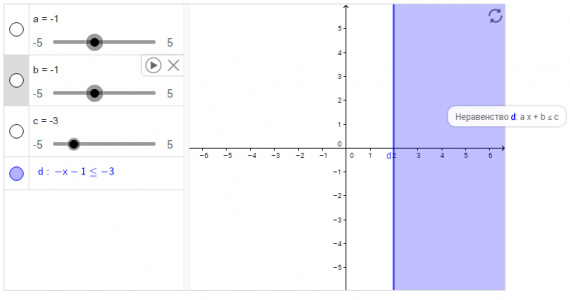
Графическое решение линейного неравенства

Исследуйте графическое решение линейного неравенства ax + b ≤ c, где a, b и c – это параметры, значения которых меняются с помощью ползунков.

ИНСТРУКЦИЯ

1		Используя виртуальную клавиатуру, введите линейное неравенство ax + b ≤ c в поле алгебраического ввода и нажмите кнопку Enter. Подсказка: GeoGebra автоматически создаст ползунки для параметров a, b и c.
2		Используя инструмент Перемещение, установите значение параметров a = 1, b = 1 и c = 3.
3		В настройках Стиля сделайте шаг ползунка равным 1. Подсказка: Выделите параметр a и откройте Панель Стилей в окне графического вида. Нажмите на значок Параметры и выберите вкладку Ползунок. Установите значение Шаг на 1. Повторите действия для параметров b и c.

Предоставлен перевод учебных материалов с официального сайта Geogebra
Источник: www.geogebra.org/b/P9fSOxh1#