GeoGebra можно использовать при изучении вопросов симметрии на уроках математики. Вы можете добавить в рабочую область любую картинку или фотографию, и с помощью инструментов симметрии GeoGebra продемонстрировать основные свойства, например, осевой симметрии.
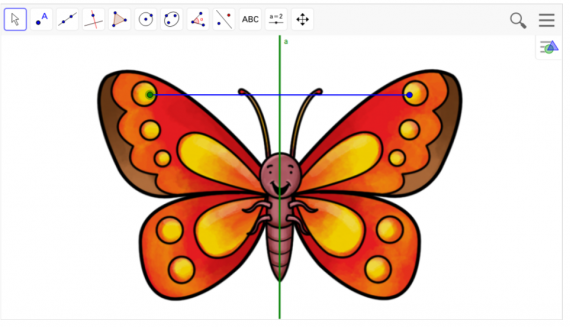 ИНСТРУКЦИЯ
ИНСТРУКЦИЯ
1. Используя галерею SMART Notebook, добавьте изображение на рабочую область виджета GeoGebra. Удерживая левую кнопку мыши выберите пункт
Закрепить объект, чтобы зафиксировать изображение на плоскости и защитить от случайных перемещений.
Подсказка: Вы также можете использовать инструмент
 Изображение
Изображение для вставки картинки в окно GeoGebra.
2. Постройте ось симметрии, используя инструмент
 Прямая
Прямая
3. Отметьте произвольную точку на объекте, используя инструмент
 Точка
Точка.
4. Используя инструмент
 Отражение
Отражение относительно прямой, постройте точку симметричную данной.
Подсказка: Вначале выделите точку, затем ось симметрии.
5. Перемещайте точку на объекте, и наблюдайте за перемещением симметричной ей точки.



 Изображение для вставки картинки в окно GeoGebra.
Изображение для вставки картинки в окно GeoGebra. Прямая
Прямая Точка.
Точка. Отражение относительно прямой, постройте точку симметричную данной.
Отражение относительно прямой, постройте точку симметричную данной. 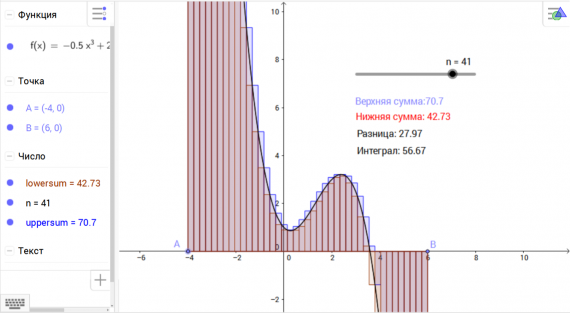
 , и укажите соответствующую переменную upsum. Нажмите кнопку ОК. Аналогично создается надпись для нижней части.
, и укажите соответствующую переменную upsum. Нажмите кнопку ОК. Аналогично создается надпись для нижней части.