GeoGebra в режиме "Стереометрия. 3D Graphics": практическая работа № 3
Динамические стереометрические фигуры
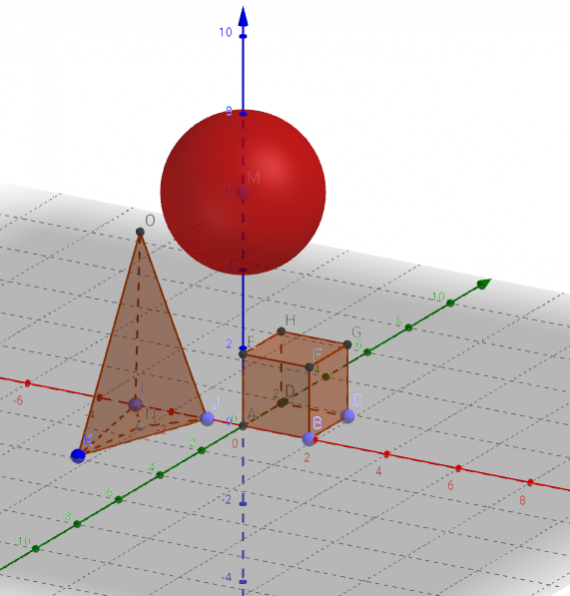
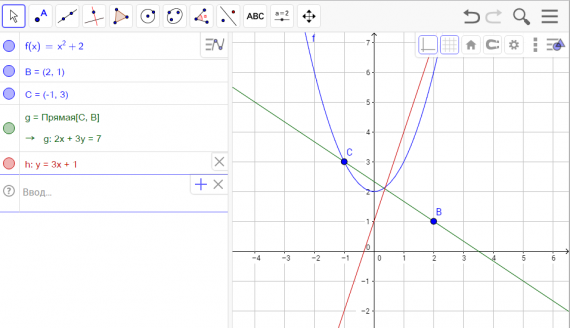
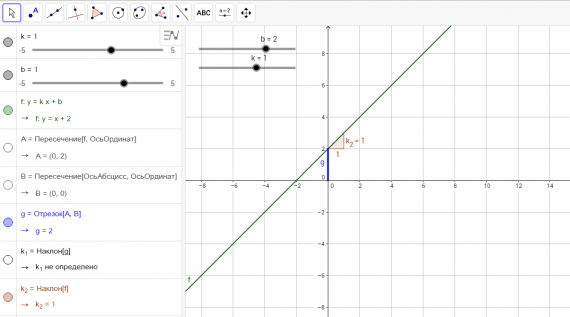
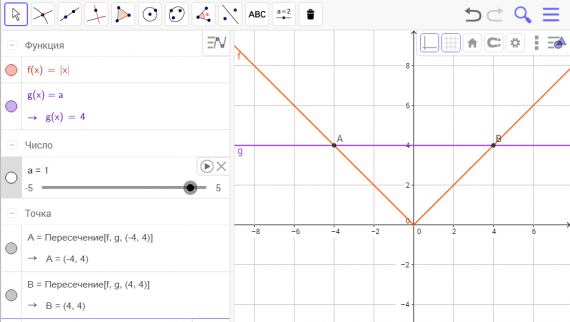
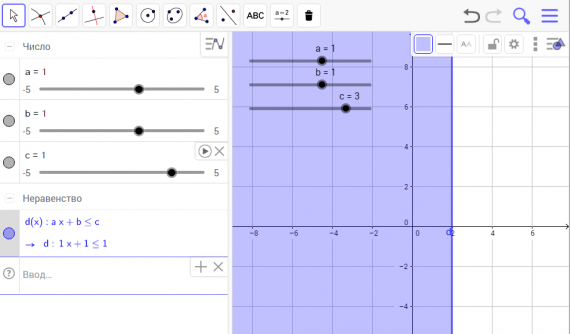
Куб, пирамида, сфера
Цилиндр и конус

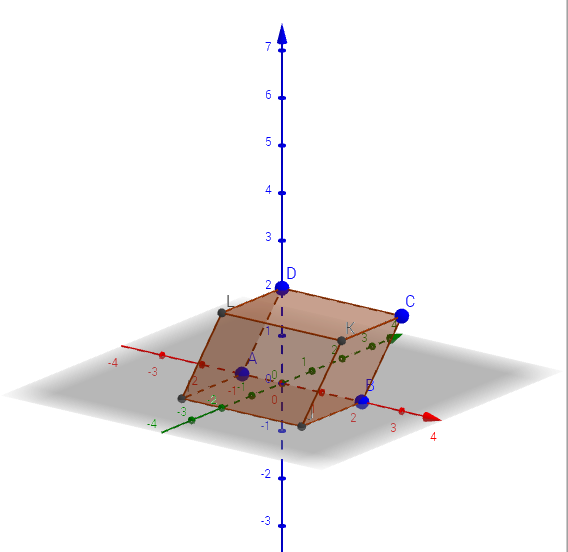
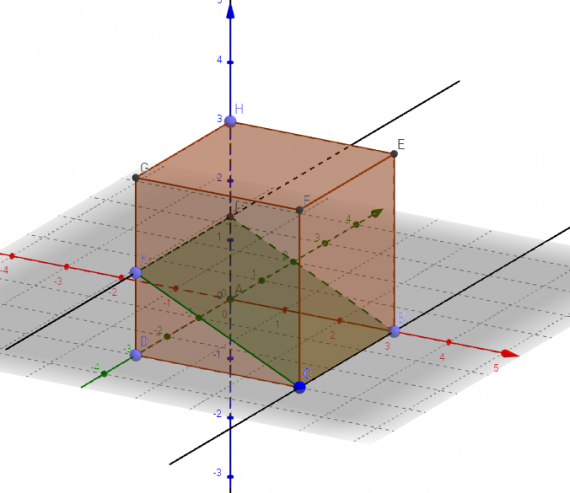
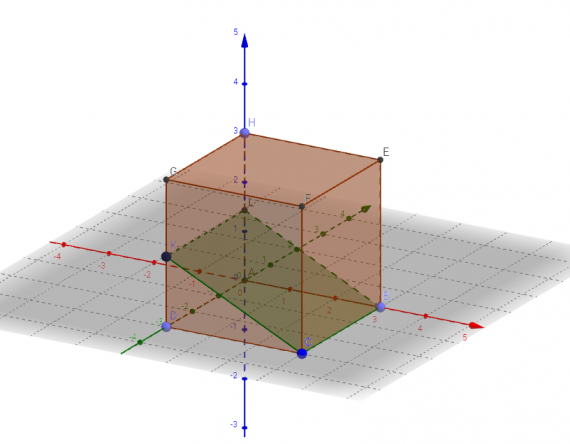
Параллелепипед
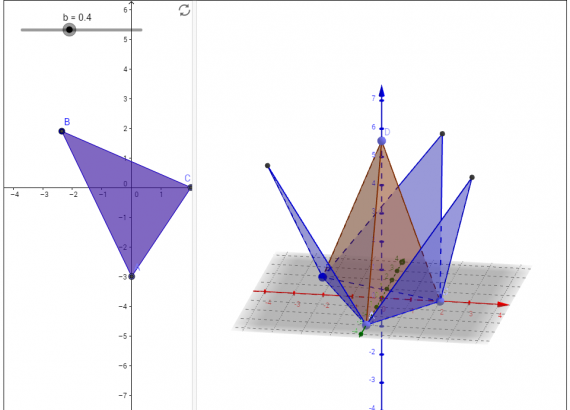
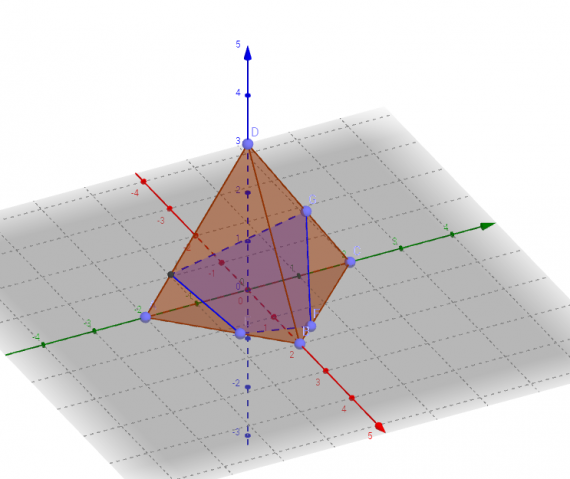
Пирамида и анимированная развертка





Всем здравствуйте! Продолжаем разговор о смешанном обучении. Если вы, уважаемые коллеги, знакомы с этой технологией или изучили информацию, перейдя по указанным ссылкам в предыдущей статье, то уже имеете представление о тех моделях, которые можно использовать в наших школах. Я ещё раз напомню, что разработана целая система моделей для средней школы. Наиболее эффективными являются модели группы «Вращение» (Rotation):
· «Сменарабочихзон» (Station-Rotation)
· «Перевернутый класс» (Flipped-Classroom)
· «Автономная группа» (Lab -Rotation)
· «Индивидуальная траектория» (Individual -Rotation)
Каждая из перечисленных моделей достойна внимания, изучения и применения. Но наиболее распространённой является модель «Перевёрнутый класс». Поэтому следующие статьи посвящены именно ей:
Образовательный портал NEWTONEW:
Блог Марины Курвитс на портале «Образовательная галактика Intel» (требуется регистрация на портале!)




В «УГ Москва», №32 от 9 августа 2016 года вышла моя статья с предложением для школ по внедрению внутринней системы оценки качества повышающей объективность школьной оотметки. Хочу привести некоторые тезисы из этой статьи.
Каждая образовательная организация стремится к повышению объективности внутренней системы оценки качества образования (ВСОКО) и судить о ее успешности в школах можно на основе независимых диагностик и итоговой государственной аттестации. Традиционная система оценки знаний, включает в себя измерение качества знаний (КЗ) и уровня успешности классов и школы в целом, измерение средней степени обученности учащихся (СОУ) классов, подсчет резерва «хорошистов» и «отличников». В то время как образовательные организации, входящие в рейтинги лучших школ, в большинстве своем, используют другие критерии. Они отказались от измерения «средней температуры по больнице», то есть не проводят измерений КЗ и СОУ 3-4 раза в год, у них нет единых аттестационных периодов для всех предметов, нет понятия резерв «хорошистов и отличников», они измеряют индивидуальные достижения каждого обучающегося с использованием контролируемых элементов содержания (КЭСов), и применяют различные шкалы системы оценивания знаний на равне с традиционной пятибалльной системой.