Высокие японские технологии или как "открыть" задачу
Японские школьники традиционно демонстрируют высокий уровень математического образования. Результаты последних международных исследований опровергли распространенный стереотип, о том, что образование в Японии сводится к зубрежке и не допускает самостоятельной деятельности. Безусловно, учащиеся школ Японии проводят за учебой значительно больше времени, чем их сверстники с Запада. Однако исследования показывают, что японские ученики превосходят своих ровесников из других стран в умении решать задачи, требующие понимания, применения полученных знаний и использования таких научных методов, как формулировка гипотез.
Как отмечает Такеши Миакава в своей статье «Опыт „хорошего“ преподавания математики», исторически обучение в японских школах, построено таким образом, что учитель играет менее заметную роль на уроке, оставляя возможность учащимся самостоятельно разрабатывать собственные алгоритмы и методы решения задач. Именно поэтому в Японии и был разработан целый ряд методик по организации исследовательской, поисковой работы учащихся, одним из которых является подход, основанный на решении открытых задач.
Истоки открытого подхода можно найти в Японии 70-х гг XX века. В период 1971-1976 гг. японские исследователи провели ряд экспериментов по проверке его эффективности на уроках математики. Выявленные положительные тенденции нашли свое отражение в трудах японского ученого, родоначальника открытого подхода Нобухико Нохда.
ОСОБЕННОСТИ ОТКРЫТОГО ПОДХОДА
Использование открытого подхода базируется на применении так называемых открытых задач — задач, которые имеют не одно, а множество правильных решений. Это обусловлено тем, что открытые задачи могут:
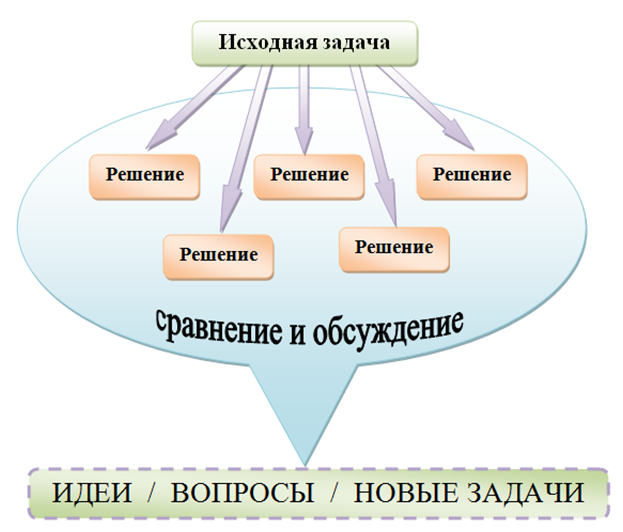
Рисунок 1. Ход решения открытой задачи
ОТКРЫТЫЕ ЗАДАЧИ
Итак, какие задачи мы можем считать открытыми? Открытые задачи – это противоположность закрытым. В открытых задачах исходные данные или конечная цель явно не заданы, учащимся дается свобода в постановке вопроса своего исследования, в выборе метода рассуждений, в введении дополнительных параметров необходимых для решения. В связи с этим, в процессе решения могут получиться совершенно разные, но абсолютно правильные результаты, в силу сделанного учащимся выбора и принятых допущений. Стоит отметить, что в реальной жизни мы сталкиваемся в основном с задачами открытого типа, трудно представить себе жизненную ситуацию, в которой были бы даны все исходные данные, четко поставлена цель и имеется только один выход из сложившей ситуации.
КЛАССИФИКАЦИЯ ОТКРЫТЫХ ЗАДАЧ
Согласно статье Н. Нохда мы можем классифицировать задачи по виду их «открытости». Таким образом, в зависимости от открытого параметра выделяются три вида задач:
• задачи с множественными ответами;
• задачи с множественными вариантами решений;
• задачи типа «от задачи к задаче».
Также в зависимости от исходных данных, смыслового содержания задачи, поставленного вопроса и времени затрачиваемого на ее решение выделяют:
• задачи-исследования;
• жизненные задачи;
• задачи без явного вопроса;
• вариативные задачи (что–если?);
• проекты.
Стоит отметить, что одна и та же задача может быть отнесена к нескольким категориям в зависимости от целей урока, уровня учащихся и пожеланий преподавателя.
РЕКОМЕНДАЦИИ ПО СОЗДАНИЮ СОБСТВЕННЫХ ЗАДАЧ ОТКРЫТОГО ТИПА
Источниками учебных открытых задач могут служить исторические факты, научные и научно-популярные книги, периодика, документальные фильмы, патентный фонд и т.д. Для того чтобы научиться составлять открытые задачи, удобно рассматривать их основные характеристики в сравнении с классическими («закрытыми») задачами (табл. 1). Тогда создание открытой задачи сводится к переформулировке (если это возможно) задачи «закрытого» типа.
Характеристики задач открытого и закрытого типа
Условие: исходных данных для решения задачи может быть недостаточно или наоборот избыточное количество.
Постановка вопроса: Что можно, а что нельзя найти по данным задачи? Нельзя ли ослабить условие? Нельзя ли усилить утверждение?
Ход решения: знаний для решения задачи недостаточно, учащемуся необходимо решать подзадачи, накапливая необходимый опыт; методов решений задачи может быть достаточно много.
Результат: «правильных» решений в задаче может быть несколько, в зависимости от того какое направление исследования было выбрано.
Открытая задача, прежде всего, отличается от классической достаточно высокой степенью свободы. В зависимости от уровня учащихся открытую задачу можно дополнять данными для того, чтобы сделать более очевидными первоначальные шаги исследования.
Применение ткрытого подхода подтвердило свою эффективность в японских школах и в школах ряда европейских странах, таких как Финляндия, Франция и Германия, а также в Таиланде и Корее.
Эксперимент в российской школе также подтвердил, что среди результатов использования открытого подхода на уроках математики стоит отметить повышение количества учащихся включенных в процесс исследования, приобретение навыков работы в группе и опыта публичной защиты своего проекта, приобретение базовых исследовательских компетенций.
Таким образом, использование открытого подхода на уроках математики своими результатами оправдывает затраты на подготовку уроков с их применением и преодоление трудностей, встречаемых на первых этапах организации новой для учащихся формы работы на уроке.
Естественно, что открытый подход является нестандартной педагогической технологией, его внедрение в образовательный процесс связано с рядом серьезных трудностей. Во-первых, это объективная неготовность педагогов к тому, что задача может иметь несколько верных решений, и вполне возможен случай, когда сам педагог не рассматривал возможность такого решения, при этом оно является абсолютно правильным. Во-вторых, до сих пор остается открытым вопрос оценивания такого рода задач. В-третьих, до сих пор не разработана методическая система, позволяющая использовать открытый подход на уроках математики во всех параллелях. Даже в Японии, это система развита на достаточном уровне только для начальной школы.
Как отмечает Такеши Миакава в своей статье «Опыт „хорошего“ преподавания математики», исторически обучение в японских школах, построено таким образом, что учитель играет менее заметную роль на уроке, оставляя возможность учащимся самостоятельно разрабатывать собственные алгоритмы и методы решения задач. Именно поэтому в Японии и был разработан целый ряд методик по организации исследовательской, поисковой работы учащихся, одним из которых является подход, основанный на решении открытых задач.
Истоки открытого подхода можно найти в Японии 70-х гг XX века. В период 1971-1976 гг. японские исследователи провели ряд экспериментов по проверке его эффективности на уроках математики. Выявленные положительные тенденции нашли свое отражение в трудах японского ученого, родоначальника открытого подхода Нобухико Нохда.
ОСОБЕННОСТИ ОТКРЫТОГО ПОДХОДА
Использование открытого подхода базируется на применении так называемых открытых задач — задач, которые имеют не одно, а множество правильных решений. Это обусловлено тем, что открытые задачи могут:
- либо содержать недостаточное количество данных и для ее решения, учащиеся самостоятельно выбирают дополняющие параметры, которые могут быть разными как по количественной характеристике, так и по сути;
- либо в задаче может быть неявно задана цель, т.е. ученик находится в ситуации, когда даже не понимает, что конкретно нужно найти в процессе решения.

Рисунок 1. Ход решения открытой задачи
ОТКРЫТЫЕ ЗАДАЧИ
Итак, какие задачи мы можем считать открытыми? Открытые задачи – это противоположность закрытым. В открытых задачах исходные данные или конечная цель явно не заданы, учащимся дается свобода в постановке вопроса своего исследования, в выборе метода рассуждений, в введении дополнительных параметров необходимых для решения. В связи с этим, в процессе решения могут получиться совершенно разные, но абсолютно правильные результаты, в силу сделанного учащимся выбора и принятых допущений. Стоит отметить, что в реальной жизни мы сталкиваемся в основном с задачами открытого типа, трудно представить себе жизненную ситуацию, в которой были бы даны все исходные данные, четко поставлена цель и имеется только один выход из сложившей ситуации.
КЛАССИФИКАЦИЯ ОТКРЫТЫХ ЗАДАЧ
Согласно статье Н. Нохда мы можем классифицировать задачи по виду их «открытости». Таким образом, в зависимости от открытого параметра выделяются три вида задач:
• задачи с множественными ответами;
• задачи с множественными вариантами решений;
• задачи типа «от задачи к задаче».
Также в зависимости от исходных данных, смыслового содержания задачи, поставленного вопроса и времени затрачиваемого на ее решение выделяют:
• задачи-исследования;
• жизненные задачи;
• задачи без явного вопроса;
• вариативные задачи (что–если?);
• проекты.
Стоит отметить, что одна и та же задача может быть отнесена к нескольким категориям в зависимости от целей урока, уровня учащихся и пожеланий преподавателя.
РЕКОМЕНДАЦИИ ПО СОЗДАНИЮ СОБСТВЕННЫХ ЗАДАЧ ОТКРЫТОГО ТИПА
Источниками учебных открытых задач могут служить исторические факты, научные и научно-популярные книги, периодика, документальные фильмы, патентный фонд и т.д. Для того чтобы научиться составлять открытые задачи, удобно рассматривать их основные характеристики в сравнении с классическими («закрытыми») задачами (табл. 1). Тогда создание открытой задачи сводится к переформулировке (если это возможно) задачи «закрытого» типа.
Характеристики задач открытого и закрытого типа
Условие: исходных данных для решения задачи может быть недостаточно или наоборот избыточное количество.
Постановка вопроса: Что можно, а что нельзя найти по данным задачи? Нельзя ли ослабить условие? Нельзя ли усилить утверждение?
Ход решения: знаний для решения задачи недостаточно, учащемуся необходимо решать подзадачи, накапливая необходимый опыт; методов решений задачи может быть достаточно много.
Результат: «правильных» решений в задаче может быть несколько, в зависимости от того какое направление исследования было выбрано.
Открытая задача, прежде всего, отличается от классической достаточно высокой степенью свободы. В зависимости от уровня учащихся открытую задачу можно дополнять данными для того, чтобы сделать более очевидными первоначальные шаги исследования.
Применение ткрытого подхода подтвердило свою эффективность в японских школах и в школах ряда европейских странах, таких как Финляндия, Франция и Германия, а также в Таиланде и Корее.
Эксперимент в российской школе также подтвердил, что среди результатов использования открытого подхода на уроках математики стоит отметить повышение количества учащихся включенных в процесс исследования, приобретение навыков работы в группе и опыта публичной защиты своего проекта, приобретение базовых исследовательских компетенций.
Таким образом, использование открытого подхода на уроках математики своими результатами оправдывает затраты на подготовку уроков с их применением и преодоление трудностей, встречаемых на первых этапах организации новой для учащихся формы работы на уроке.
Естественно, что открытый подход является нестандартной педагогической технологией, его внедрение в образовательный процесс связано с рядом серьезных трудностей. Во-первых, это объективная неготовность педагогов к тому, что задача может иметь несколько верных решений, и вполне возможен случай, когда сам педагог не рассматривал возможность такого решения, при этом оно является абсолютно правильным. Во-вторых, до сих пор остается открытым вопрос оценивания такого рода задач. В-третьих, до сих пор не разработана методическая система, позволяющая использовать открытый подход на уроках математики во всех параллелях. Даже в Японии, это система развита на достаточном уровне только для начальной школы.

0 комментариев