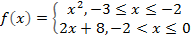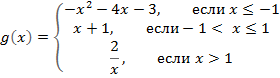С помощью GeoGebra и инструмента захват экрана SMART вы можете создать увлекательную игру «Функциональное домино» для своих учеников. Она поможет учащимся запомнить соответствие алгебраической записи функции и её графика.

Система компьютерной алгебры (СКА, англ. computer algebra system, CAS) — это прикладная программа для символьных вычислений, то есть выполнения преобразований и работы с математическими выражениями в аналитической (символьной) форме.

Сегодня мы поговорим о возможностях Geogebra по проведению компьютерного эксперимента. Стоит отметить, что под компьютерным экспериментом здесь понимается разновидность модельного эксперимента, в котором в качестве объекта изучения выступает динамический чертеж (модель).

Режим Геометрия соответствует Графическому виду режима Алгебра и графики, за исключением отсутствия координатных прямых по умолчанию, и предназначена для проведения геометрических построений на плоскости.

Панель инструментов

Панель инструментов в режиме Геометрия также полностью совпадает с панелью графического вида в режиме Алгебра и графики:

Инструменты объединены в группы по типу создаваемых объектов, а подсказки, возникающие в нижней части окна GeoGebra при выборе того или иного инструмента, помогут вам при использовании незнакомого инструмента.

Знакомство с некоторыми инструментами

1		Выберите инструмент Прямая и кликните в окне графического вида, для создания точек А и В, через которые будет проходить прямая.
2		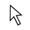Выберите инструмент Указатель и поменяйте положение точки.
3		Найдите инструмент Наклон прямой и выберите прямую, чтобы отобразить наклон.
4		Выберите инструмент Окружность по центр и радиусу, прочитайте подсказку и постройте окружность с центром в точке А, радиусом 4.
5		Используйте инструмент Отрезок с фиксированной длиной, для создания отрезка длиной 3.
6		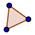Постройте треугольник, используя инструмент Многоугольник. Подсказка: Нажмите на первую точку снова для завершения построения многоугольника.
7		Постройте точку внутри треугольника, используя инструмент Точка на объекте.
8		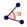С помощью инструмента Угол, измерьте угол между любыми тремя точками, последовательно выбирая их против часовой стрелки.
9		Используйте инструмент Показать/скрыть объект для скрытия с экрана треугольника.

Использование команд

В режиме геометрия использование команд возможно только при добавлении Строки ввода через пункт Основного меню – Вид
Правила написания команд совпадают с описанными ранее.
Более детальную информацию можно получить через пункт Основного меню – Справка – и выбрав пункт Manual. Руководство содержит дельную информацию по всем командам GeoGebra, но пока доступно только на английском языке.

Попробуйте самостоятельно:

1. Построить параллелограмм, используя инструменты Параллельная прямая и Пересечение
2. Постройте квадрат, используя инструменты Перпендикулярная прямая, Окружность, Пересечение, Многоугольник
3. Постройте окружность, описанную вокруг треугольника, используя инструмент Срединный перпендикуляр

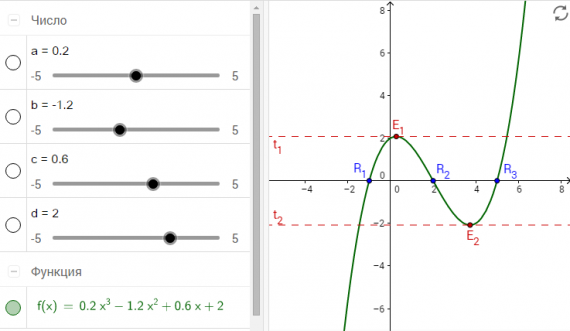
Сегодня мы рассмотрим возможности Geogebra по исследованию графиков функции: нахождение нулей и экстремумов, а также построение касательной к точке экстремума.
Исследуйте график кубической функции f(x) = a x³ + b x² + c x + d, где a, b, c и d – это параметры, значения которых меняются с помощью ползунков.

Сегодня мы рассмотрим построение кусочных функций в режиме Алгебра и графики виджета Geogebra.
Нам необходимо построить графики следующих функций:

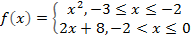
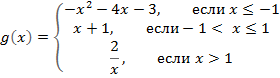
Сегодня мы рассмотрим несколько вариантов использования ползунка в Geogebra:
1. Изучение графика линейной функции
2. Построение графика функции с модулем f(x) = |x| и изучение точек пересечения с графиком функции g(x)=a
3. Графическое решение линейного неравенства ax + b ≤ c

При добавлении виджета GeoGebra на страницу SMART Notebook, по умолчанию загружается режим работы Алгебра и графика. В этом режиме рабочая область разделена на две части Алгебраический вид и Графический вид.
В Алгебраическом виде отображаются количественные характеристики объекта: координаты – для точки, длина – для отрезка, площадь – для плоской фигуры, объем – для стереометрических объектов, для прямых и кривых – описывающие их уравнения. Также с помощью Алгебраического вида осуществляется ввод команд для задания объектов, а в Графическом виде моментально осуществляется построение данных объектов. Вы можете строить объекты в окне Графического вида непосредственно на координатной плоскости с помощью мыши, используя панель инструментов.
Таким образом, работая в режиме Алгебра и графика, можно наглядно показать взаимосвязь между алгебраическим представлением объекта и его геометрической интерпретацией.
Рассмотрим различные варианты построений в режиме Алгебра и графики.

Добавление GeoGebra в SMART Notebook

1. Нажмите кнопку Add-ons («Надстройки») , затем нажмите GeoGebra.
2. Выберите пункт «Вставить виджет GeoGebra»

Если вы хотите использовать материалы из коллекции GeoGebraTube, введите ключевое слово в поле «Поиск в материалах GeoGebra», а затем нажмите «Поиск». На текущей странице SMART Notebook появится рабочий лист.

Кевин Вербах — автор книги «Вовлекай и властвуй» и первого в мире курса по геймификации на образовательной платформе coursera.org, является родоначальником методологии геймификации в бизнесе. В образовании эта технология также набирает обороты и является одним из наиболее перспективных направлений. Ведь ее основная цель — повышение мотивации, что является одной из наиболее актуальных проблем современного образования.

В своей книге Кевин Вербах подробно описывает шестиэтапную схему геймификации, о которой и пойдет речь. Схема носит название D6, в русском переводе обычно обозначается О6 (шесть «О»). Мы рассмотрим ее в контексте образования и отметим, что несколько изменили порядок следования: этапы 2 и 3 мы поменяли местами. Потому что на наш взгляд, очерчивать желательное поведение игроков, легче после того как вы их описали. Но обо всем по порядку.