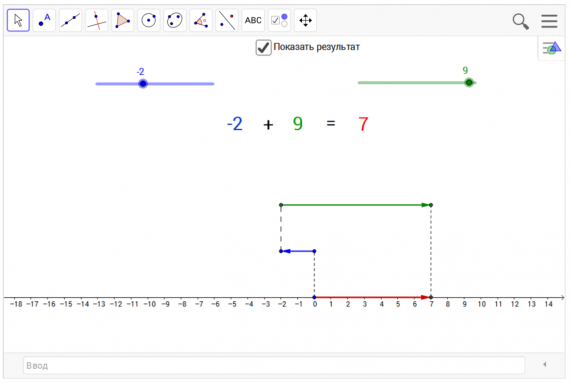
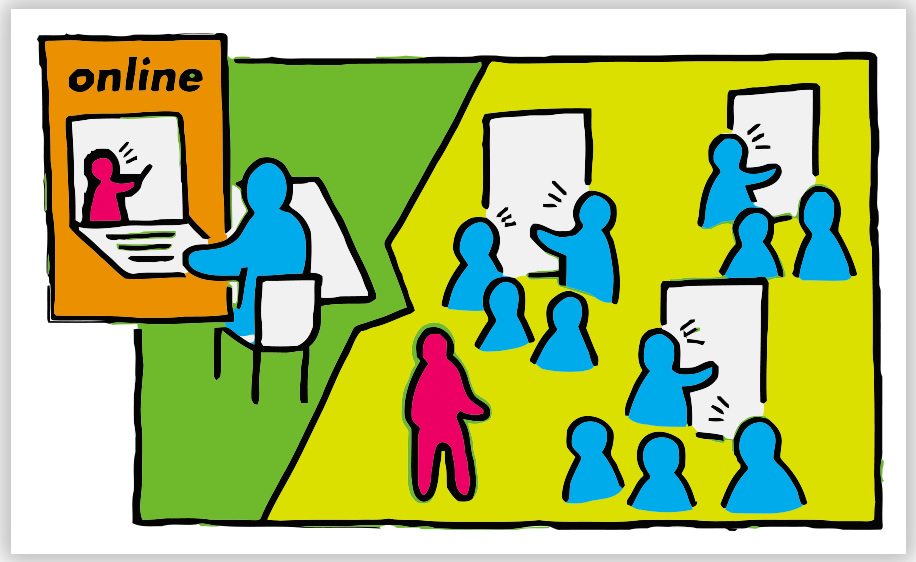
Работа в режиме Геометрия
Режим Геометрия соответствует Графическому виду режима Алгебра и графики, за исключением отсутствия координатных прямых по умолчанию, и предназначена для проведения геометрических построений на плоскости.

Инструменты объединены в группы по типу создаваемых объектов, а подсказки, возникающие в нижней части окна GeoGebra при выборе того или иного инструмента, помогут вам при использовании незнакомого инструмента.
 Основного меню –
Основного меню –  Вид
Вид
Правила написания команд совпадают с описанными ранее.
Более детальную информацию можно получить через пункт Основного меню –
Основного меню –  Справка – и выбрав пункт Manual. Руководство содержит дельную информацию по всем командам GeoGebra, но пока доступно только на английском языке.
Справка – и выбрав пункт Manual. Руководство содержит дельную информацию по всем командам GeoGebra, но пока доступно только на английском языке.
Панель инструментов
Панель инструментов в режиме Геометрия также полностью совпадает с панелью графического вида в режиме Алгебра и графики:
Инструменты объединены в группы по типу создаваемых объектов, а подсказки, возникающие в нижней части окна GeoGebra при выборе того или иного инструмента, помогут вам при использовании незнакомого инструмента.
Знакомство с некоторыми инструментами
| 1 |  | Выберите инструмент Прямая и кликните в окне графического вида, для создания точек А и В, через которые будет проходить прямая. |
| 2 |  | Выберите инструмент Указатель и поменяйте положение точки. |
| 3 |  | Найдите инструмент Наклон прямой и выберите прямую, чтобы отобразить наклон. |
| 4 |  | Выберите инструмент Окружность по центр и радиусу, прочитайте подсказку и постройте окружность с центром в точке А, радиусом 4. |
| 5 |  | Используйте инструмент Отрезок с фиксированной длиной, для создания отрезка длиной 3. |
| 6 |  | Постройте треугольник, используя инструмент Многоугольник. Подсказка: Нажмите на первую точку снова для завершения построения многоугольника. |
| 7 |  | Постройте точку внутри треугольника, используя инструмент Точка на объекте. |
| 8 |  | С помощью инструмента Угол, измерьте угол между любыми тремя точками, последовательно выбирая их против часовой стрелки. |
| 9 |  | Используйте инструмент Показать/скрыть объект для скрытия с экрана треугольника. |
Использование команд
В режиме геометрия использование команд возможно только при добавлении Строки ввода через пункт Основного меню –
Основного меню –  Вид
ВидПравила написания команд совпадают с описанными ранее.
Более детальную информацию можно получить через пункт
 Основного меню –
Основного меню –  Справка – и выбрав пункт Manual. Руководство содержит дельную информацию по всем командам GeoGebra, но пока доступно только на английском языке.
Справка – и выбрав пункт Manual. Руководство содержит дельную информацию по всем командам GeoGebra, но пока доступно только на английском языке.Попробуйте самостоятельно:
- Построить параллелограмм, используя инструменты Параллельная прямая и Пересечение
- Постройте квадрат, используя инструменты Перпендикулярная прямая, Окружность, Пересечение, Многоугольник
- Постройте окружность, описанную вокруг треугольника, используя инструмент Срединный перпендикуляр