Объясняшка: "Как SMART board помогает понять трудные темы в 1 классе!"
«Объясняшка»!
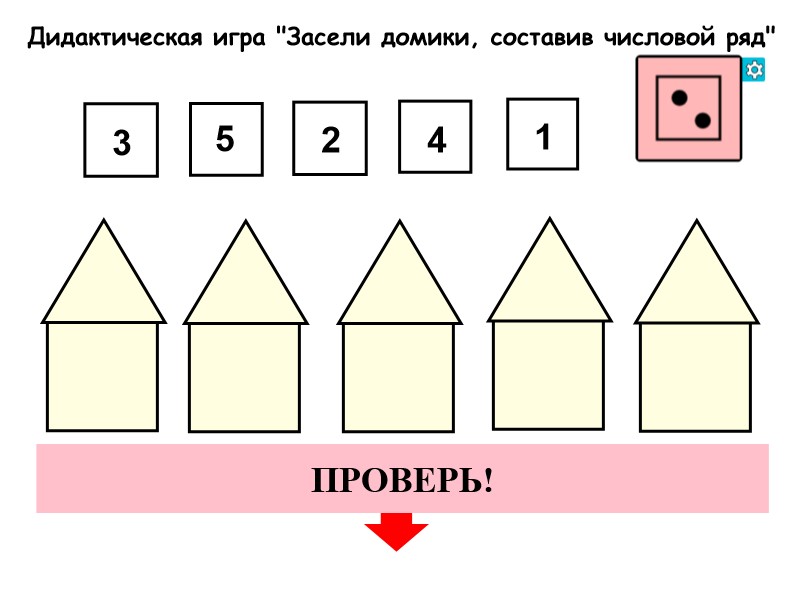
В этом видеоролике первоклассники объясняют решение трудных задач. Иногда дети не сразу понимают трудную тему урока. Мы решили, что ученики лучше всего могут понять объяснение одноклассников. А может кто-то болел, и это видео ему поможет понять решение! И SMART board детям очень помогает!
В этом видеоролике первоклассники объясняют решение трудных задач. Иногда дети не сразу понимают трудную тему урока. Мы решили, что ученики лучше всего могут понять объяснение одноклассников. А может кто-то болел, и это видео ему поможет понять решение! И SMART board детям очень помогает!
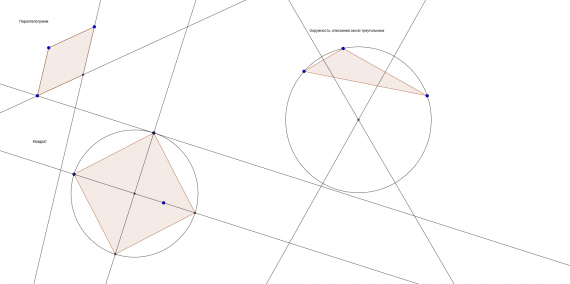


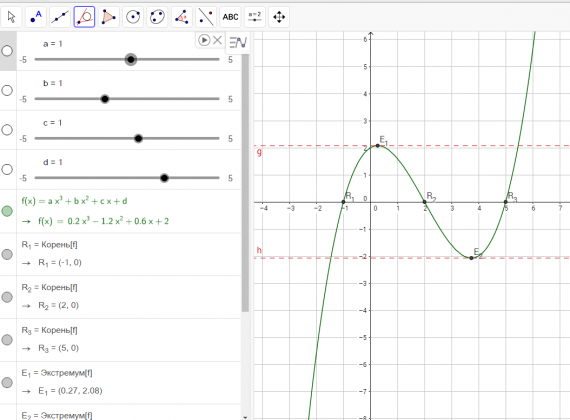
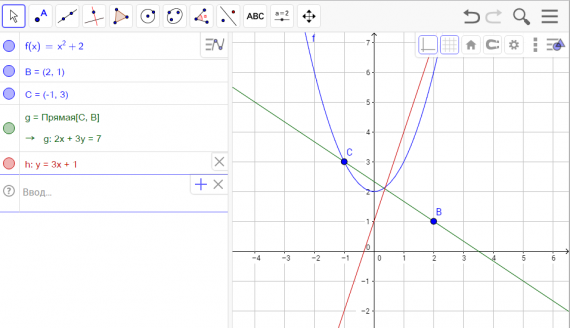
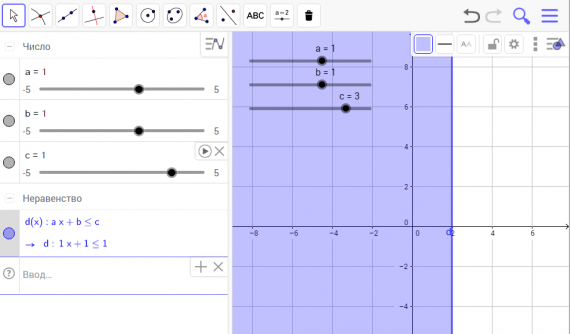
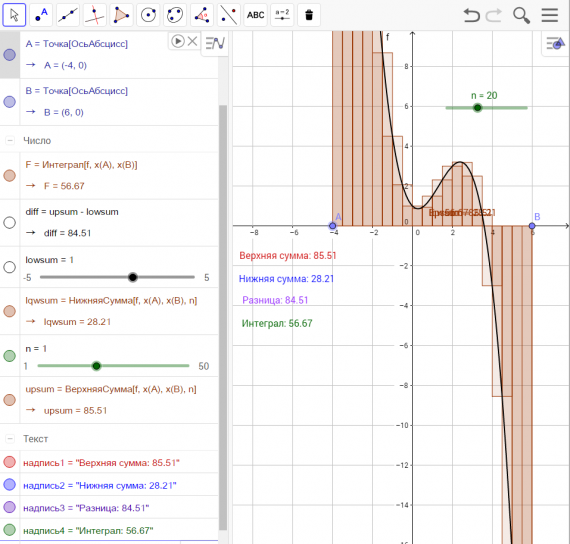

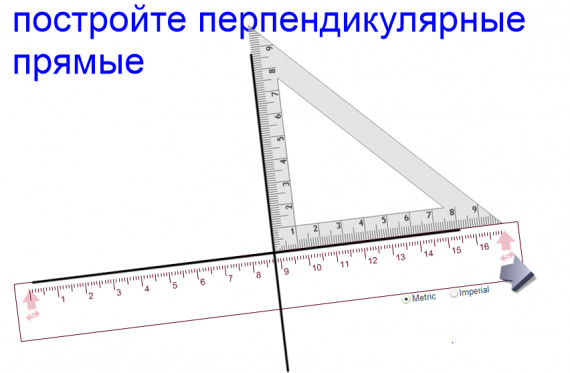
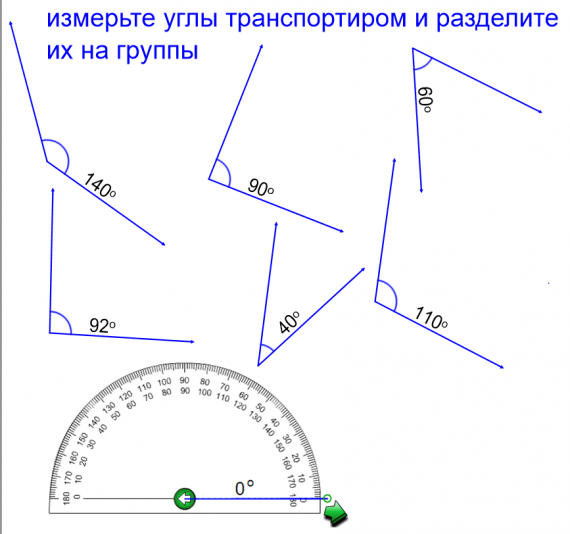
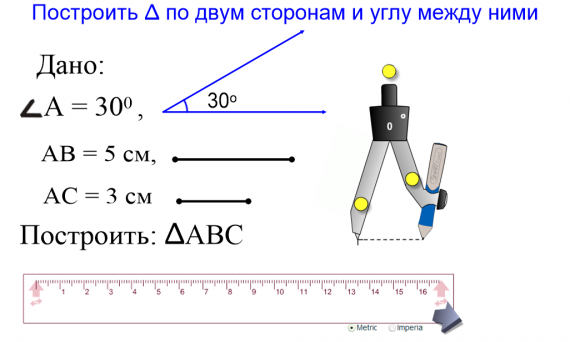
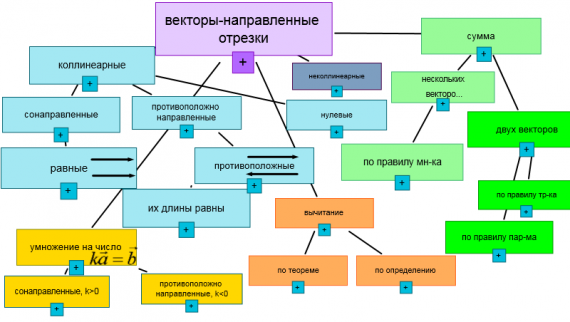
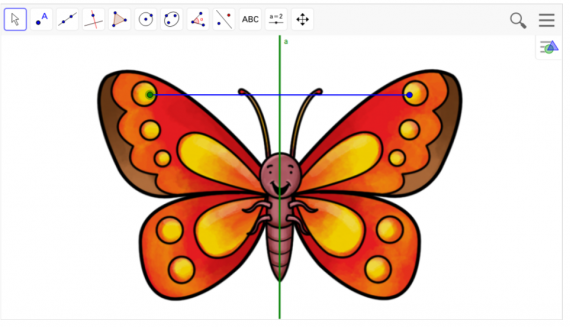
 Изображение для вставки картинки в окно GeoGebra.
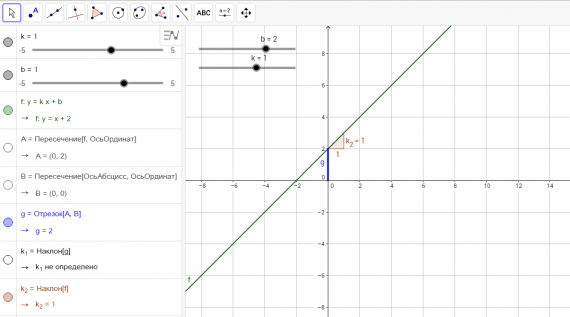
Изображение для вставки картинки в окно GeoGebra. Прямая
Прямая Точка.
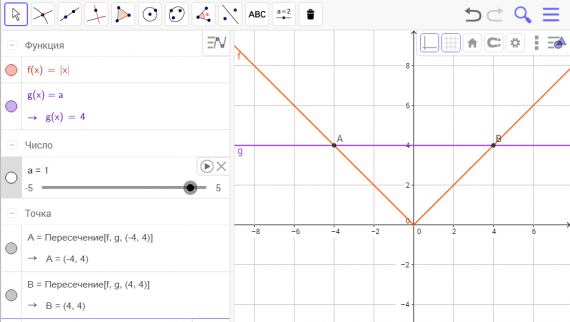
Точка.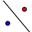 Отражение относительно прямой, постройте точку симметричную данной.
Отражение относительно прямой, постройте точку симметричную данной.