GeoGebra в режиме "CAS": практическая работа № 5
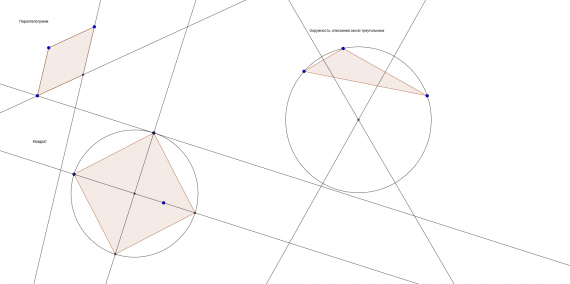
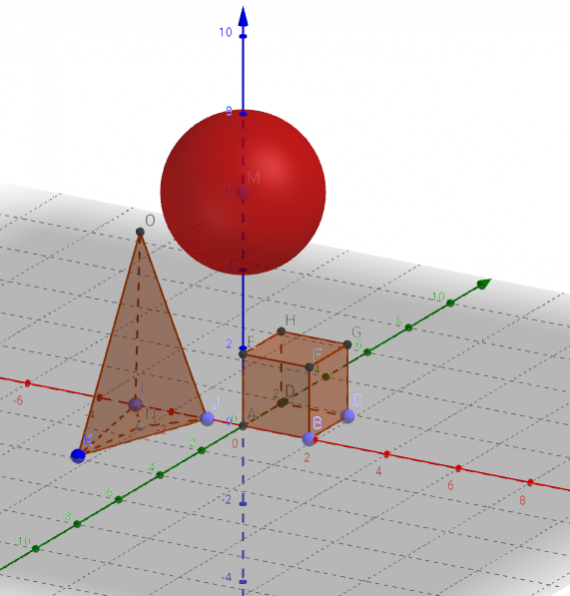
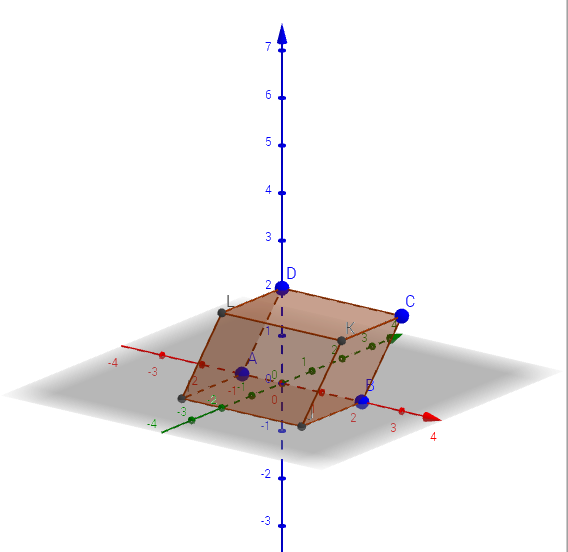
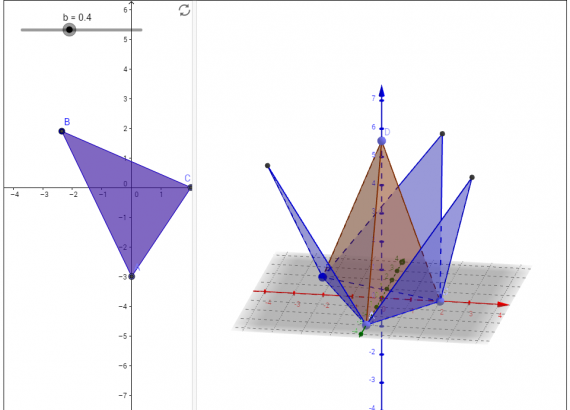
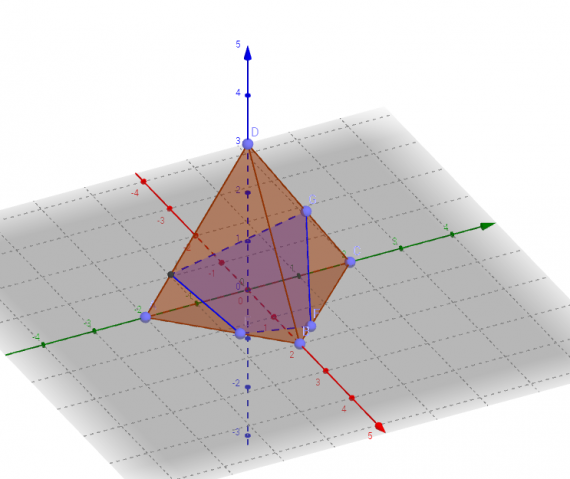
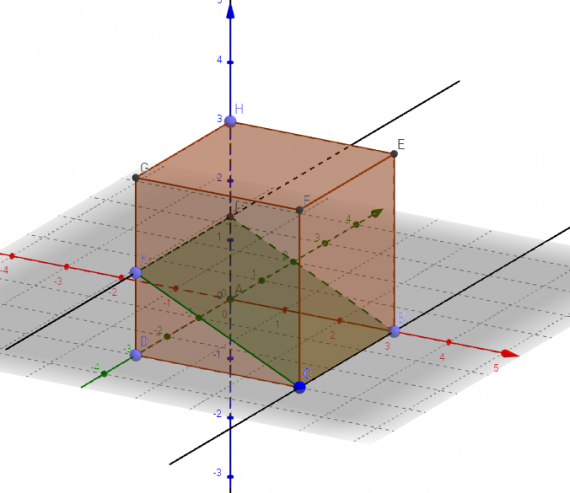
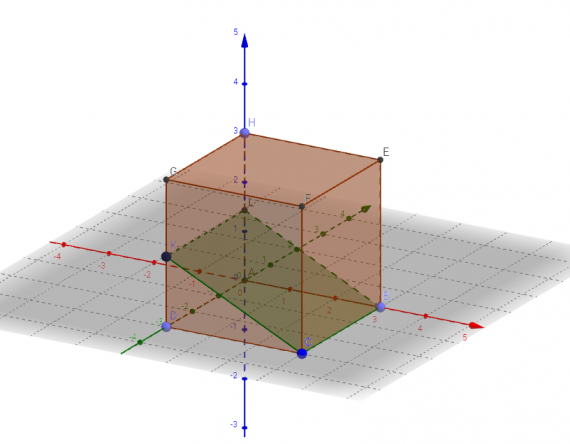
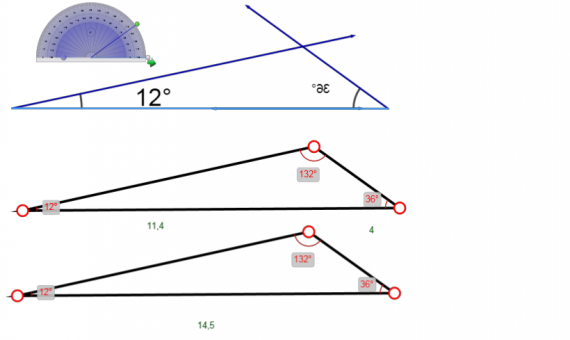
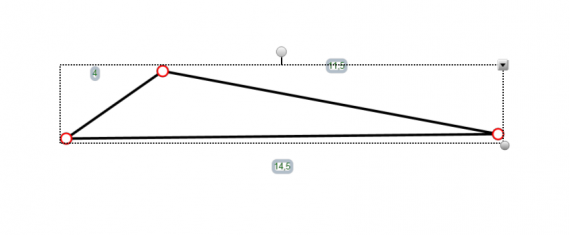
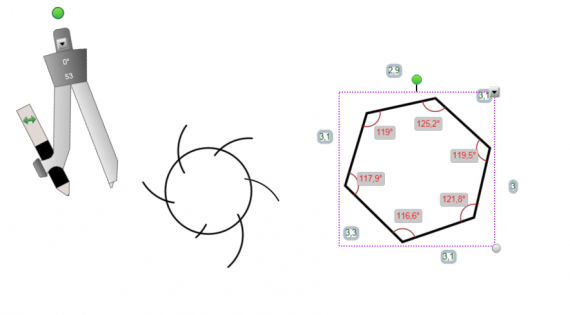
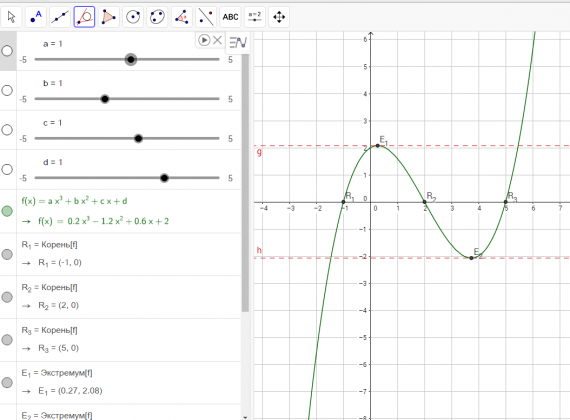
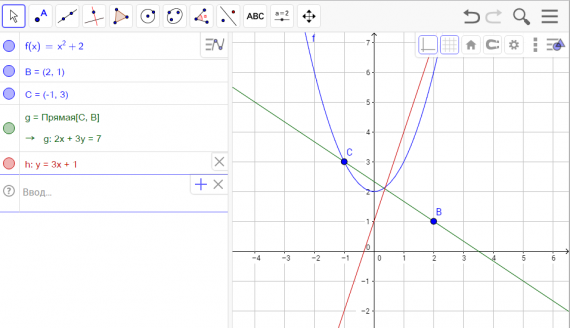
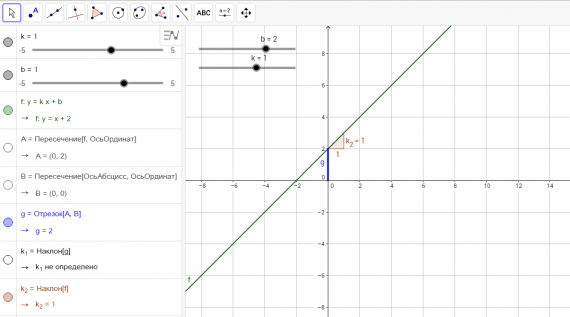
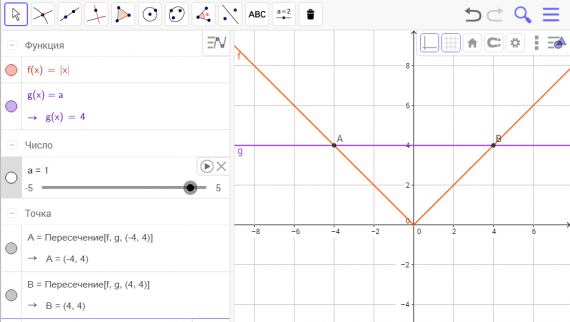
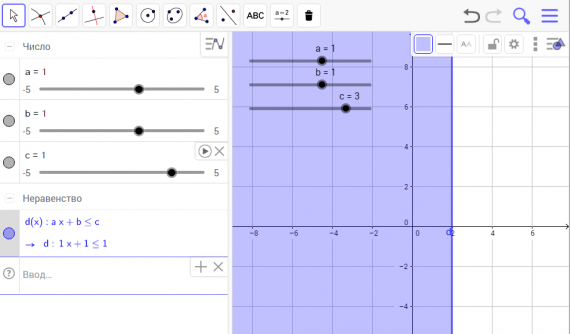
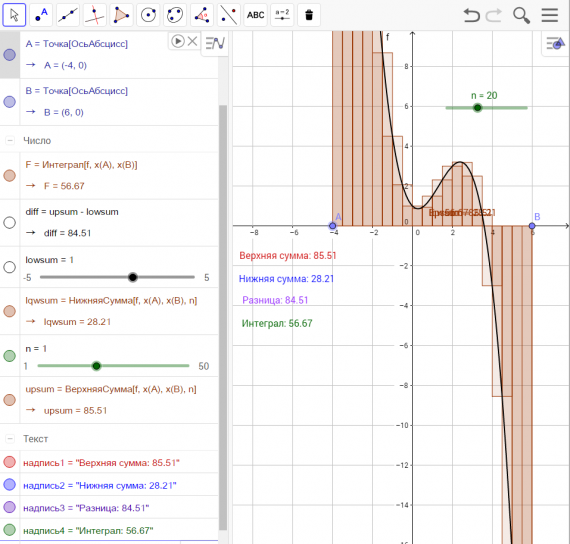
В приложении GeoGebra режиме CAS — система компьютерной алгебры — при выполнении практики по заданию Летней школы SMART выполнялись следующие задачи: программировать и проверять преобразование алгебраических выражений, находить значения буквенных выражений при введённых значениях букв, вычислять НОД и НОК чисел, решать уравнения, вычислять производную, строить графики и даже вычислять матрицы.
Практическая работа № 5
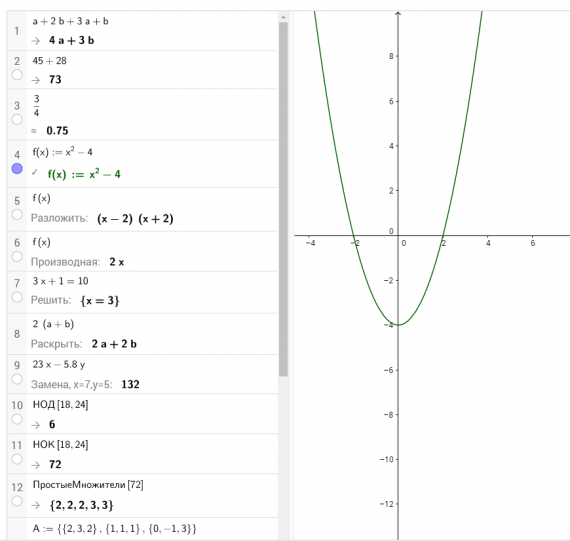
Практическая работа № 5