Введение понятия интеграла
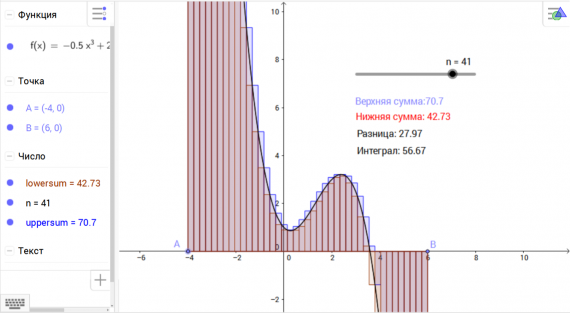
Режим Алгебра и Графики удобно использовать для введения новых понятий, в том числе и понятия интеграла. В этом упражнении мы рассмотрим вопрос вычисления площади криволинейной трапеции и введения понятия определенного интеграла, причем подойдем к нему в геометрическом смысле.
ИНСТРУКЦИЯ

ИНСТРУКЦИЯ
- Введите в поле алгебраического ввода уравнение произвольной кубической функции, например: f(x) = -0.5x³ + 2x² — x + 1 и нажмите кнопку Enter.
Подсказка: GeoGebra автоматически создаст ползунки для параметров - Отметьте точки A и B на оси абсцисс, используя инструмент
 Точка.
Точка. - Создайте ползунок n, используя инструмент
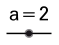 Ползунок. Установите минимальное значение 1, а максимальное – 50, с шагом 1.
Ползунок. Установите минимальное значение 1, а максимальное – 50, с шагом 1. - Введите команду upsum = UpperSum[f,x(A),x(B),n] и команду lowsum = LowerSum[f,x(A),x(B),n] для вычисления верхней и нижней суммы Дарбу.
Подсказка: x(A) – возвращает координату точки А по оси абсцисс - Создайте динамический текст для отображения на экране верхней и нижней суммы. Используя инструмент
 Надпись, создайте текстовое поле, введите текст «Верхняя сумма:», а затем в окне Дополнительно выберите вкладку
Надпись, создайте текстовое поле, введите текст «Верхняя сумма:», а затем в окне Дополнительно выберите вкладку  , и укажите соответствующую переменную upsum. Нажмите кнопку ОК. Аналогично создается надпись для нижней части.
, и укажите соответствующую переменную upsum. Нажмите кнопку ОК. Аналогично создается надпись для нижней части. - Вычислите разность diff=upsum-lowsum и добавьте соответствующий динамический текст.
- Вычислите интеграл F=Integral[f, x(A), x(B)] и добавьте соответствующий динамический текст.
- Зафиксируйте текст и ползунок на рабочей области, воспользовавшись пунктом Закрепить всплывающего меню.
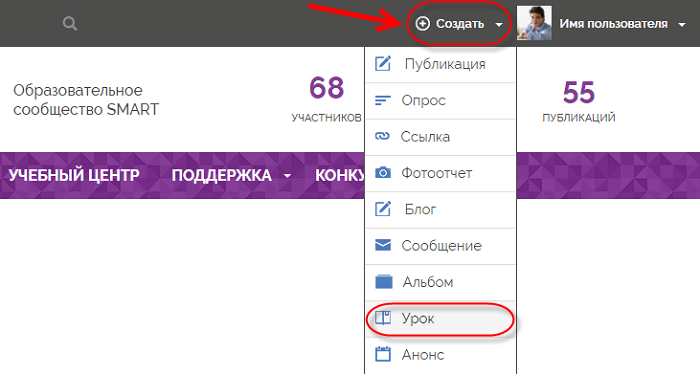 … или перейдите в раздел УРОКИ в главном меню
… или перейдите в раздел УРОКИ в главном меню  и кликните по красной надписи «Добавление урока».
и кликните по красной надписи «Добавление урока». 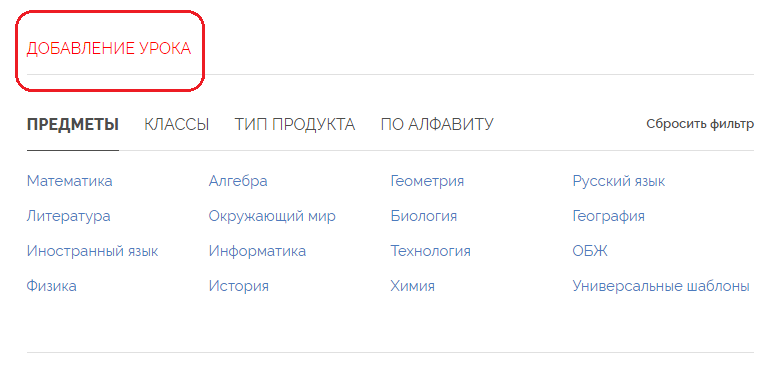 В обоих случаях откроется страница редактирования публикации урока на вкладке "Основное".
В обоих случаях откроется страница редактирования публикации урока на вкладке "Основное". 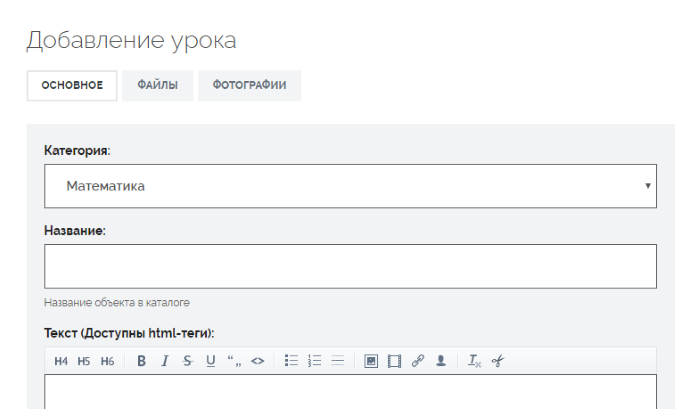 Укажите:
Укажите: Для размещения скриншотов наиболее интересных фрагментов Вашего урока перейдите на вкладку "Фотографии". Рекомендуемое количество — не более пяти.
Для размещения скриншотов наиболее интересных фрагментов Вашего урока перейдите на вкладку "Фотографии". Рекомендуемое количество — не более пяти. 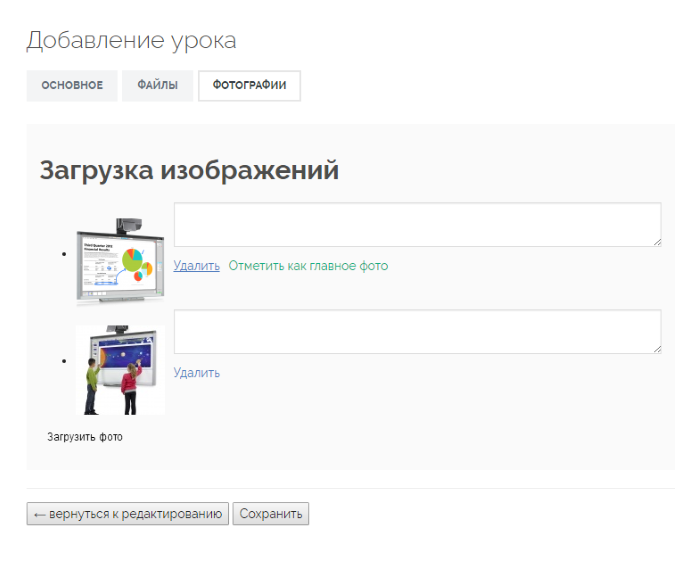 Обязательно загрузите титульную страницуВашего ЭОРа и сделайте её главной фотографией.
Обязательно загрузите титульную страницуВашего ЭОРа и сделайте её главной фотографией. Далее нажмите на кнопку:
Далее нажмите на кнопку:  После модерации Ваш урок будет доступен в БИБЛИОТЕКЕ РЕСУРСОВ EdGuru.RU.
После модерации Ваш урок будет доступен в БИБЛИОТЕКЕ РЕСУРСОВ EdGuru.RU.