Математический инструментарий SMART. Темы 1-4. Общий математический инструментарий.
Вот несколько примеров.
1) С помощью блоков показываем, как устроены числа Фибоначчи.
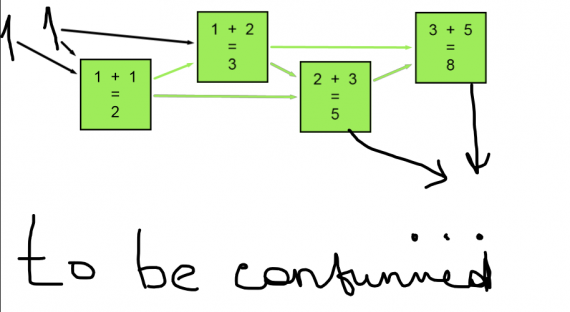
2) С помощью транспортира и инструмента многоугольник строим треугольник с углами 36, 12 и 132. Он примечателен тем, что является контрпримером к «неправильному» признаку равнобедренности треугольника по равным биссектрисам двух внешних углов.
Показываем углы и длины сторон треугольника для следующего примера.
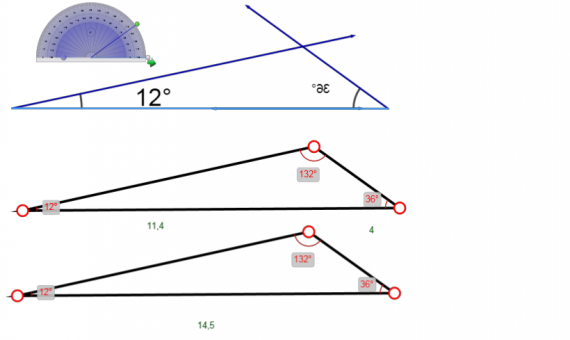
3) С помощью инструмента Многоугольник и пункта Показать вершины и Показать стороны строим треугольник со сторонами из примера 3. Интересно чисто технически подогнать под стороны, т.к. это не так уж и просто (попробуйте сами, отобразите углы после построения). Ну и сам треугольник мы уже отмечали. Его «контрпримерность» возможно обсудим в одной из следующих публикаций.
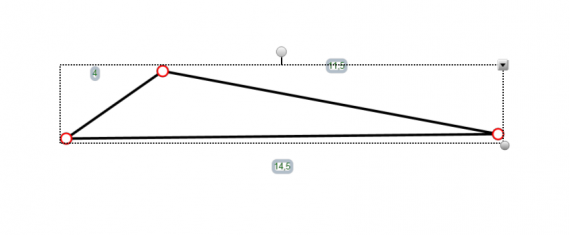
4) Ну и напоследок строим правильный шестиугольник с помощью циркуля. Если отобразить стороны, то видно, что он не совсем и правильный получился..
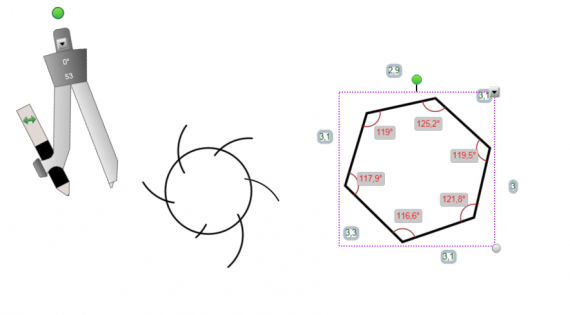
1) С помощью блоков показываем, как устроены числа Фибоначчи.

2) С помощью транспортира и инструмента многоугольник строим треугольник с углами 36, 12 и 132. Он примечателен тем, что является контрпримером к «неправильному» признаку равнобедренности треугольника по равным биссектрисам двух внешних углов.
Показываем углы и длины сторон треугольника для следующего примера.

3) С помощью инструмента Многоугольник и пункта Показать вершины и Показать стороны строим треугольник со сторонами из примера 3. Интересно чисто технически подогнать под стороны, т.к. это не так уж и просто (попробуйте сами, отобразите углы после построения). Ну и сам треугольник мы уже отмечали. Его «контрпримерность» возможно обсудим в одной из следующих публикаций.

4) Ну и напоследок строим правильный шестиугольник с помощью циркуля. Если отобразить стороны, то видно, что он не совсем и правильный получился..
